Intro
Unlock the power of calculus with our step-by-step guide to finding the derivative of 9x. Learn the rules of differentiation, including the power rule and constant multiple rule, to confidently calculate the derivative of linear functions. Master the concept of derivatives and enhance your math skills with this easy-to-follow tutorial.
Finding the derivative of a function is a fundamental concept in calculus, and it's essential to master this skill to succeed in mathematics and science. In this article, we'll focus on calculating the derivative of 9x, a simple yet essential function.
What is a Derivative?
Before diving into the calculation, let's briefly review what a derivative is. A derivative measures how a function changes as its input changes. It's a measure of the rate of change of the function with respect to one of its variables. In the context of the function 9x, the derivative will tell us the rate at which the output changes when the input x changes.
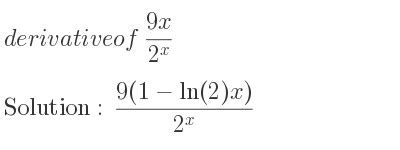
Calculating the Derivative of 9x
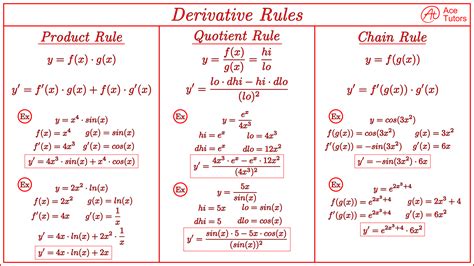
To calculate the derivative of 9x, we'll apply the power rule of differentiation. The power rule states that if we have a function of the form f(x) = x^n, then the derivative is f'(x) = nx^(n-1).
In this case, the function is 9x, which can be rewritten as 9x^1. Applying the power rule, we get:
f'(x) = 9(1)x^(1-1) f'(x) = 9x^0
Since x^0 is equal to 1, the derivative simplifies to:
f'(x) = 9

Interpretation of the Derivative
Now that we've calculated the derivative, let's interpret the result. The derivative tells us that the rate of change of the function 9x is constant and equal to 9. This means that for every unit change in x, the output changes by 9 units.
In practical terms, if we're dealing with a real-world problem involving the function 9x, the derivative can help us understand how changes in the input variable affect the output.
Geometric Interpretation of the Derivative
To visualize the derivative, let's consider the geometric interpretation. The derivative represents the slope of the tangent line to the graph of the function at a given point. In the case of 9x, the graph is a straight line with a slope of 9.
Important Notes on the Derivative of 9x
- The derivative of 9x is a constant function, which means that the rate of change is the same at every point.
- The derivative is not defined at x = 0, since the function is not differentiable at this point.
- The derivative of 9x is an example of a linear function, which means that the graph is a straight line.
Derivative of 9x Image Gallery



What is the derivative of 9x?
+The derivative of 9x is 9.
Why is the derivative of 9x important?
+The derivative of 9x is important because it helps us understand how changes in the input variable affect the output.
Is the derivative of 9x a linear function?
+Yes, the derivative of 9x is a linear function, which means that the graph is a straight line.
In conclusion, calculating the derivative of 9x is a straightforward process using the power rule of differentiation. The derivative represents the rate of change of the function and is essential for understanding how changes in the input variable affect the output. We hope this article has helped you understand the concept of the derivative and its application to the function 9x.
