Mastering George Mason Calculus 3: A Comprehensive Guide

Mastering calculus is a vital skill for any student pursuing a degree in mathematics, physics, engineering, or computer science. George Mason University's Calculus 3 course is a challenging but rewarding experience that helps students develop a deep understanding of multivariable calculus. In this comprehensive guide, we will provide an overview of the course, its objectives, and offer practical tips and strategies for mastering the subject.

Calculus 3 is a fundamental course that builds upon the concepts learned in Calculus 1 and 2. The course focuses on the study of multivariable calculus, including vectors, vector-valued functions, partial derivatives, double and triple integrals, and differential equations. By the end of the course, students will be able to apply these concepts to solve problems in physics, engineering, and other fields.

Understanding the Course Objectives

The primary objectives of George Mason University's Calculus 3 course are to:

• Develop an understanding of vectors and vector-valued functions
• Learn to compute partial derivatives and use them to solve optimization problems
• Understand the concept of multiple integrals and apply them to solve problems in physics and engineering
• Develop skills in solving differential equations and apply them to model real-world phenomena
• Cultivate problem-solving skills and critical thinking

Mastering Vectors and Vector-Valued Functions

Vectors and vector-valued functions are fundamental concepts in Calculus 3. To master these topics, students should focus on the following:

• Understand the definition and properties of vectors
• Learn to compute vector operations such as addition, scalar multiplication, and dot product
• Study the concept of vector-valued functions and learn to compute their derivatives and integrals
• Practice solving problems involving vectors and vector-valued functions

Vector Operations

• Addition: u + v = (u1 + v1, u2 + v2,..., un + vn)
• Scalar multiplication: cu = (cu1, cu2,..., cun)
• Dot product: u · v = u1v1 + u2v2 +... + unvn

Partial Derivatives and Optimization

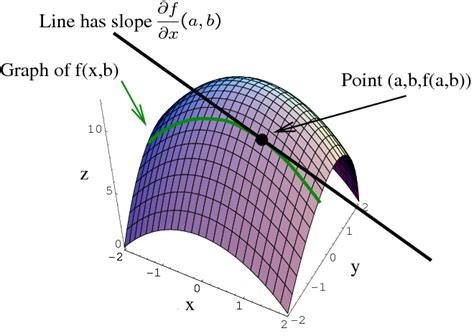
Partial derivatives are used to study the behavior of functions of multiple variables. To master partial derivatives, students should focus on the following:

• Understand the definition and notation of partial derivatives
• Learn to compute partial derivatives using the power rule, product rule, and quotient rule
• Study the concept of optimization and learn to use partial derivatives to solve optimization problems
• Practice solving problems involving partial derivatives and optimization

Partial Derivatives

• fx(x, y) = ∂f/∂x = f(x + h, y) - f(x, y)/h
• fy(x, y) = ∂f/∂y = f(x, y + h) - f(x, y)/h

Multiple Integrals

Multiple integrals are used to compute the area and volume of regions in multiple dimensions. To master multiple integrals, students should focus on the following:

• Understand the definition and notation of multiple integrals
• Learn to compute multiple integrals using the Fubini's theorem and the Jacobian
• Study the concept of change of variables and learn to use it to simplify multiple integrals
• Practice solving problems involving multiple integrals

Multiple Integrals

• ∫∫R f(x, y) dA = ∫∫D f(x(u, v), y(u, v)) |∂(x, y)/∂(u, v)| du dv

Differential Equations

Differential equations are used to model the behavior of complex systems. To master differential equations, students should focus on the following:

• Understand the definition and notation of differential equations
• Learn to solve differential equations using separation of variables, integrating factor, and undetermined coefficients
• Study the concept of linear systems and learn to use them to solve differential equations
• Practice solving problems involving differential equations

Differential Equations

• dy/dx = f(x, y)
• y' + P(x)y = Q(x)

Calculus 3 Image Gallery

What is the primary objective of George Mason University's Calculus 3 course?

+

The primary objective of George Mason University's Calculus 3 course is to develop an understanding of multivariable calculus, including vectors, vector-valued functions, partial derivatives, double and triple integrals, and differential equations.

How do I master vectors and vector-valued functions in Calculus 3?

+

To master vectors and vector-valued functions, focus on understanding the definition and properties of vectors, computing vector operations, and studying the concept of vector-valued functions and their derivatives and integrals.

What is the difference between partial derivatives and optimization in Calculus 3?

+

Partial derivatives are used to study the behavior of functions of multiple variables, while optimization is the process of finding the maximum or minimum value of a function subject to certain constraints.

We hope this comprehensive guide has provided you with a deeper understanding of George Mason University's Calculus 3 course and the skills and knowledge required to master it. By following the tips and strategies outlined in this article, you will be well on your way to achieving success in Calculus 3 and beyond.