Intro
Discover the prime factorization of 105 with our easy-to-follow, step-by-step guide. Learn how to break down 105 into its prime factors, including the prime numbers 3, 5, and 7. Understand the concept of prime factorization and how its used in mathematics, and master this fundamental skill with our simple, straightforward approach.
The concept of prime factorization is a fundamental idea in number theory, and it has numerous applications in various fields, including mathematics, computer science, and cryptography. In this article, we will explore the prime factorization of 105, a relatively small number, but one that still requires a systematic approach to break down into its prime factors.
Understanding the concept of prime factorization is essential for anyone interested in mathematics, as it helps to identify the building blocks of numbers and reveals the underlying structure of the number system. By mastering this concept, you will gain a deeper understanding of how numbers work and how they can be manipulated.
Before we dive into the prime factorization of 105, let's quickly review what prime factorization is. Prime factorization is the process of expressing a composite number as a product of prime numbers. A prime number is a positive integer that is divisible only by itself and 1, whereas a composite number is a positive integer that has at least one positive divisor other than 1 and itself.

Step-by-Step Guide to Prime Factorization of 105
The prime factorization of 105 involves a series of steps that help us identify the prime factors of the number. Here's a step-by-step guide to prime factorizing 105:
Step 1: Find the Smallest Prime Factor
The first step in prime factorizing 105 is to find the smallest prime factor of the number. We can start by dividing 105 by the smallest prime number, which is 2. However, 105 is an odd number, so we can immediately move on to the next prime number, which is 3.
Step 2: Divide by the Smallest Prime Factor
Now that we've identified 3 as a potential prime factor, we can divide 105 by 3. The result of this division is 35.
105 ÷ 3 = 35
Step 3: Find the Next Prime Factor
Next, we need to find the next prime factor of 105. Since we've already divided 105 by 3, we can focus on the result of that division, which is 35. We can start by dividing 35 by the smallest prime number, which is 2. However, 35 is an odd number, so we can move on to the next prime number, which is 5.
Step 4: Divide by the Next Prime Factor
Now that we've identified 5 as a potential prime factor, we can divide 35 by 5. The result of this division is 7.
35 ÷ 5 = 7
Step 5: Check if the Result is Prime
Now that we've divided 35 by 5, we need to check if the result, which is 7, is a prime number. Since 7 is indeed a prime number, we can conclude that the prime factorization of 105 is complete.
The prime factorization of 105 is:
105 = 3 × 5 × 7
Benefits of Prime Factorization
Prime factorization has numerous benefits, both theoretical and practical. Here are some of the most significant advantages of prime factorization:
Simplifying Complex Calculations
Prime factorization can simplify complex calculations by breaking down large numbers into their prime factors. This can make it easier to perform arithmetic operations, such as multiplication and division, by reducing the size of the numbers involved.
Understanding Number Properties
Prime factorization can help us understand the properties of numbers, such as their divisibility, primality, and congruence. By analyzing the prime factors of a number, we can gain insights into its underlying structure and behavior.
Cryptography and Security
Prime factorization plays a critical role in cryptography and security, particularly in the development of secure encryption algorithms. Many encryption techniques, such as RSA, rely on the difficulty of prime factorization to ensure secure data transmission.
Computer Science and Programming
Prime factorization has numerous applications in computer science and programming, particularly in algorithms and data structures. By using prime factorization, developers can optimize their code and improve the performance of their algorithms.
Gallery of Prime Factorization Images
Prime Factorization Image Gallery


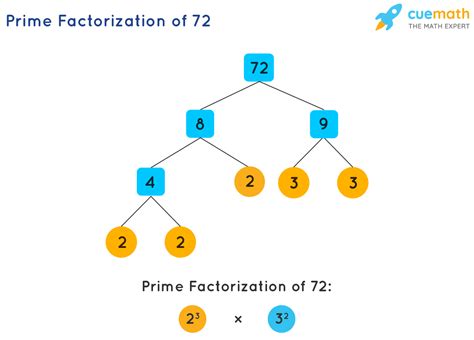
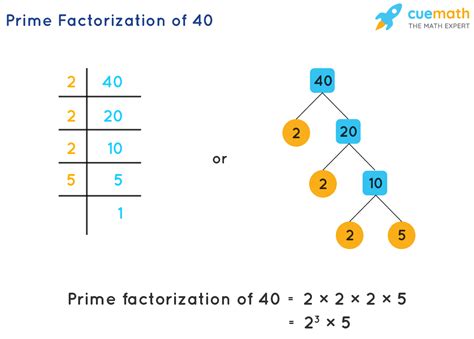

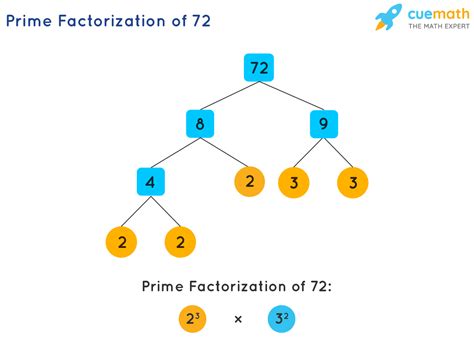

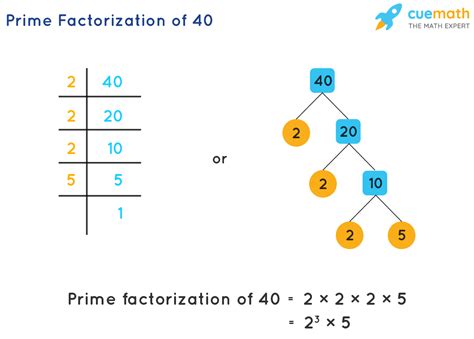

Frequently Asked Questions
What is prime factorization?
+Prime factorization is the process of expressing a composite number as a product of prime numbers.
Why is prime factorization important?
+Prime factorization is important because it helps us understand the properties of numbers, simplifies complex calculations, and has numerous applications in cryptography and security.
How do I find the prime factors of a number?
+To find the prime factors of a number, you can start by dividing the number by the smallest prime number, which is 2. If the number is divisible by 2, you can continue dividing by 2 until it is no longer divisible. Then, move on to the next prime number, which is 3, and repeat the process.
What is the prime factorization of 105?
+The prime factorization of 105 is 3 × 5 × 7.
Can I use prime factorization to simplify complex calculations?
+Yes, prime factorization can help simplify complex calculations by breaking down large numbers into their prime factors, making it easier to perform arithmetic operations.
By following the steps outlined in this article, you can easily prime factorize 105 and understand the underlying structure of the number. Prime factorization is a fundamental concept in mathematics, and its applications extend far beyond the realm of numbers. By mastering this concept, you will gain a deeper understanding of how numbers work and how they can be manipulated.
We hope this article has helped you understand the prime factorization of 105 and its significance in mathematics. If you have any questions or need further clarification, please don't hesitate to ask.
