Prime Factorization Of 130 Made Easy

Learning about prime factorization can be a bit daunting at first, but with the right approach, it can become a breeze. In this article, we'll explore the concept of prime factorization using the number 130 as an example. By the end of this article, you'll be able to find the prime factorization of 130 and understand the underlying principles.

What is Prime Factorization?

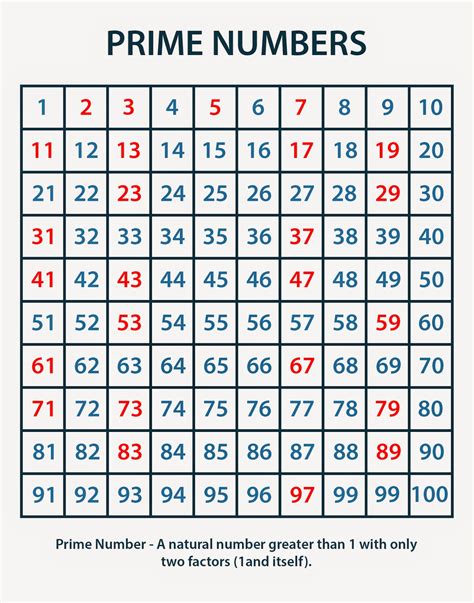
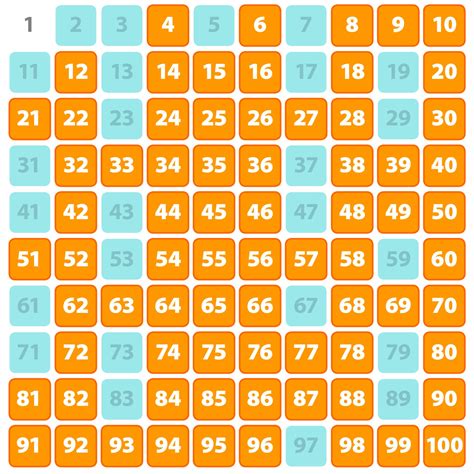
Prime factorization is a mathematical technique used to break down a composite number into its prime factors. Prime numbers are numbers that have exactly two distinct positive divisors: 1 and itself. For example, 2, 3, 5, and 7 are all prime numbers. Composite numbers, on the other hand, can be divided by other numbers besides 1 and themselves.

Why is Prime Factorization Important?

Prime factorization has numerous applications in mathematics, computer science, and cryptography. It's used to solve complex problems, such as factoring large numbers, testing primality, and finding the greatest common divisor (GCD) of two numbers. Additionally, prime factorization is a fundamental concept in number theory, which is crucial for understanding many mathematical concepts.

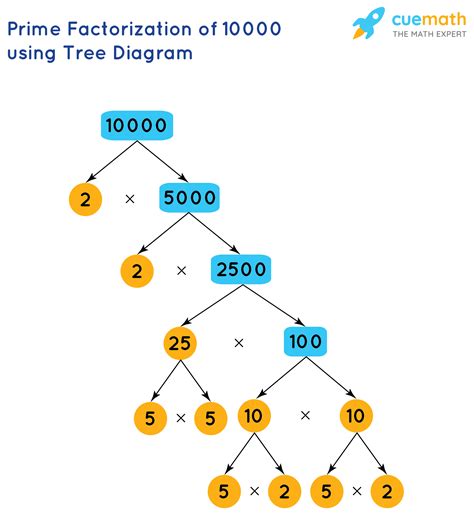
How to Find the Prime Factorization of 130

To find the prime factorization of 130, we'll use a step-by-step approach. We'll start by dividing 130 by the smallest prime number, which is 2.

Step 1: Divide 130 by 2

130 ÷ 2 = 65

Since 65 is not divisible by 2, we'll move on to the next prime number, which is 3. However, 65 is not divisible by 3 either. The next prime number is 5.

Step 2: Divide 65 by 5

65 ÷ 5 = 13

Now we have the prime factorization of 130: 2 × 5 × 13.

Verification

To verify our answer, we can multiply the prime factors together to ensure we get the original number.

2 × 5 × 13 = 130

Indeed, we get the original number 130, which confirms our prime factorization.

Why is 2 × 5 × 13 the Prime Factorization of 130?

The prime factorization of 130 is 2 × 5 × 13 because these are the prime numbers that multiply together to give us 130. The prime factorization is unique, meaning that there's only one way to express 130 as a product of prime numbers.

Benefits of Prime Factorization

Prime factorization has numerous benefits in mathematics and computer science. Some of the advantages include:

Simplifying Complex Problems: Prime factorization can simplify complex problems by breaking them down into smaller, more manageable parts.
Finding GCD: Prime factorization can be used to find the greatest common divisor (GCD) of two numbers.
Testing Primality: Prime factorization can be used to test whether a number is prime or composite.
Cryptography: Prime factorization is used in cryptography to secure online transactions and communication.

Real-World Applications

Prime factorization has many real-world applications, including:

Computer Security: Prime factorization is used in computer security to secure online transactions and communication.
Codebreaking: Prime factorization was used to break the German Enigma code during World War II.
Mathematical Research: Prime factorization is used in mathematical research to study the properties of numbers and develop new mathematical theories.

Conclusion

In this article, we've explored the concept of prime factorization using the number 130 as an example. We've learned how to find the prime factorization of 130 and understood the underlying principles. Prime factorization is a fundamental concept in mathematics and computer science, with numerous benefits and real-world applications. By mastering prime factorization, you'll be able to solve complex problems and gain a deeper understanding of mathematical concepts.

Gallery of Prime Factorization