Intro
Discover the concept of semicircle center of mass in a simple and easy-to-understand explanation. Learn how to calculate the center of mass of a semicircle, and explore related concepts such as moment of inertia, radius of gyration, and centroid. Ideal for physics students and engineers seeking a clear understanding of semicircle dynamics.
The concept of center of mass is a fundamental idea in physics and engineering, and it's essential to understand it to solve problems related to statics and dynamics. One specific case that can be tricky to analyze is the semicircle. In this article, we'll delve into the world of semicircle center of mass, exploring its definition, calculation methods, and practical applications.
What is Center of Mass?

The center of mass (COM) is the point where the entire mass of an object can be considered to be concentrated for the purpose of analyzing its motion. It's a crucial concept in understanding how objects behave under the influence of external forces. For simple shapes like triangles, rectangles, or circles, finding the center of mass is relatively straightforward. However, for more complex shapes like semicircles, the calculation can be more involved.
What is a Semicircle?
A semicircle is a two-dimensional shape that consists of half of a circle. It's a closed shape with a curved boundary and a straight edge. Semicircles are commonly found in architecture, engineering, and design, where they're used to create visually appealing and functional structures.
Types of Semicircles
There are two main types of semicircles:
- Full semicircle: A full semicircle is a shape that consists of half of a full circle.
- Partial semicircle: A partial semicircle is a shape that consists of a portion of a circle that's less than half.
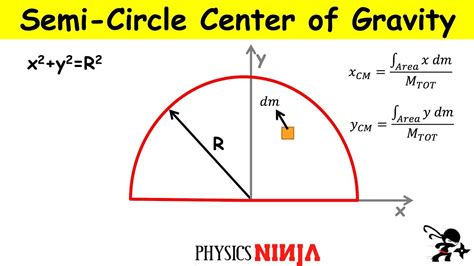
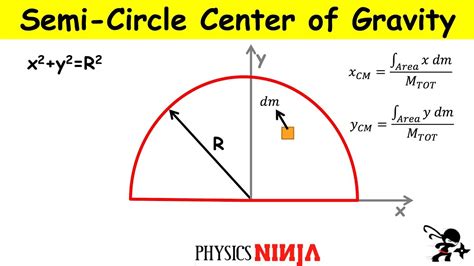
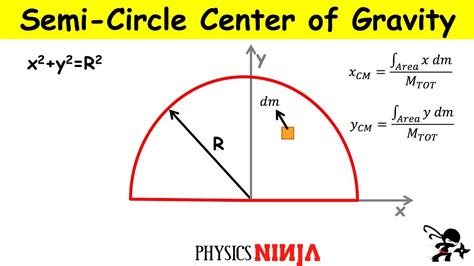
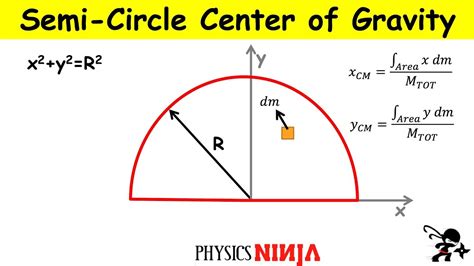
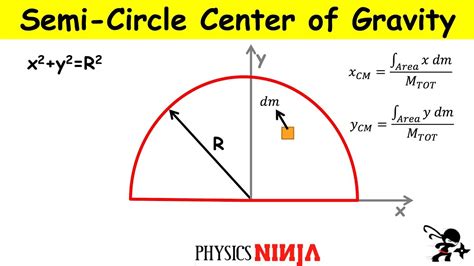
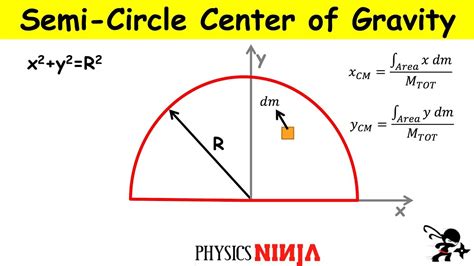
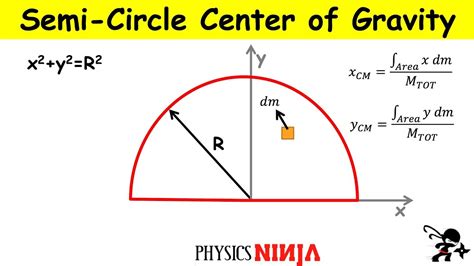
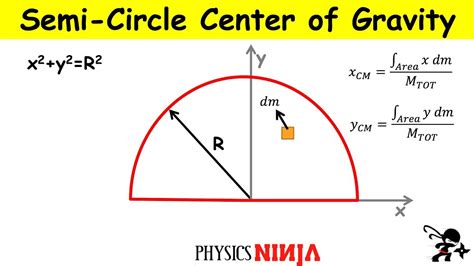
How to Calculate the Center of Mass of a Semicircle
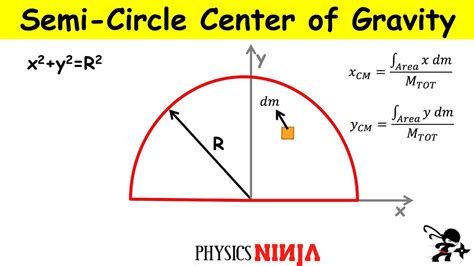
Calculating the center of mass of a semicircle involves using the following formula:
- x-coordinate: The x-coordinate of the center of mass is given by the formula: x = (2 * r * sin(θ)) / (3 * θ), where r is the radius of the circle and θ is the angle subtended by the semicircle at the center of the circle.
- y-coordinate: The y-coordinate of the center of mass is given by the formula: y = (2 * r * (1 - cos(θ))) / (3 * θ).
Practical Applications of Semicircle Center of Mass
The concept of semicircle center of mass has numerous practical applications in various fields, including:
- Engineering: Semicircles are commonly used in the design of bridges, arches, and other structural elements.
- Architecture: Semicircles are used in the design of buildings, monuments, and other architectural structures.
- Physics: Semicircles are used to model the motion of objects in circular orbits.
Gallery of Semicircle Center of Mass
Semicircle Center of Mass Images
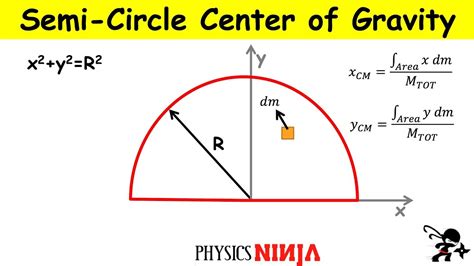
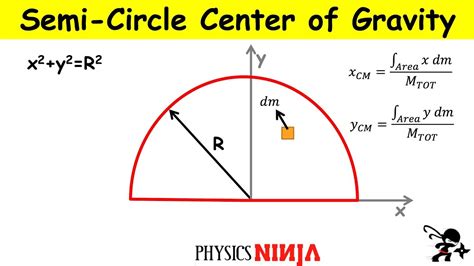
Frequently Asked Questions
What is the center of mass of a semicircle?
+The center of mass of a semicircle is the point where the entire mass of the semicircle can be considered to be concentrated for the purpose of analyzing its motion.
How do you calculate the center of mass of a semicircle?
+The center of mass of a semicircle can be calculated using the formulas: x = (2 \* r \* sin(θ)) / (3 \* θ) and y = (2 \* r \* (1 - cos(θ))) / (3 \* θ), where r is the radius of the circle and θ is the angle subtended by the semicircle at the center of the circle.
What are some practical applications of semicircle center of mass?
+The concept of semicircle center of mass has numerous practical applications in various fields, including engineering, architecture, and physics.
Now that you've learned about the concept of semicircle center of mass, take a moment to reflect on its significance in various fields. From engineering to physics, understanding the center of mass of a semicircle can help you analyze and solve complex problems. Share your thoughts and insights in the comments section below, and don't hesitate to ask if you have any questions or need further clarification on any of the topics discussed in this article.
