Intro
Discover 5 ways Youngs Inequality impacts mathematical analysis, including convex functions, integral calculus, and optimization techniques, revealing its significance in applied mathematics and real-world applications.
The concept of Young's inequality is a fundamental principle in mathematics, particularly in the field of functional analysis and inequality theory. It has far-reaching implications in various areas, including calculus, linear algebra, and optimization techniques. Young's inequality is named after the mathematician William Henry Young, who first introduced it in the early 20th century. In this article, we will delve into the concept of Young's inequality and explore its significance in mathematics.
Young's inequality states that for any non-negative real numbers $a$ and $b$, and any positive real numbers $p$ and $q$ such that $\frac{1}{p} + \frac{1}{q} = 1$, the following inequality holds: $ab \leq \frac{a^p}{p} + \frac{b^q}{q}$. This inequality has numerous applications in mathematics, physics, and engineering, and is a crucial tool for establishing bounds and limits in various mathematical contexts.
Introduction to Young's Inequality
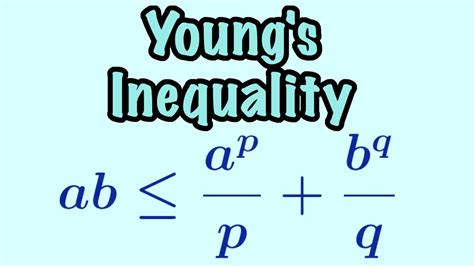
Applications of Young's Inequality
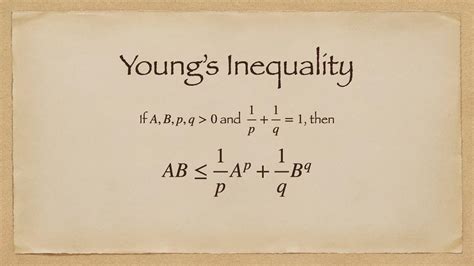
Proof of Young's Inequality
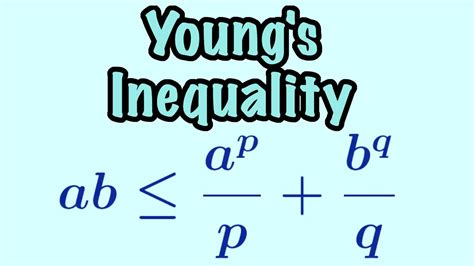
Generalizations of Young's Inequality
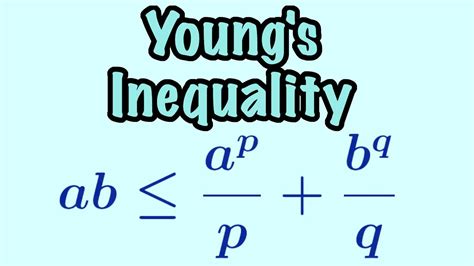
Conclusion and Future Directions
Young's Inequality Image Gallery


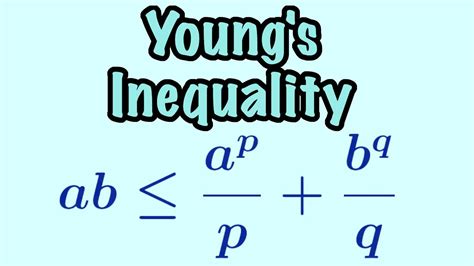


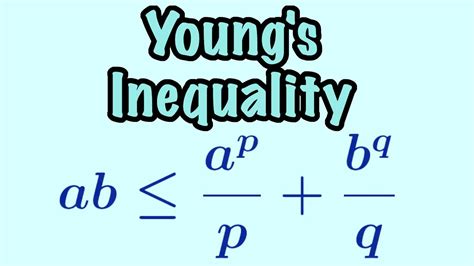


What is Young's inequality?
+Young's inequality is a mathematical principle that states that for any non-negative real numbers $a$ and $b$, and any positive real numbers $p$ and $q$ such that $\frac{1}{p} + \frac{1}{q} = 1$, the following inequality holds: $ab \leq \frac{a^p}{p} + \frac{b^q}{q}$.
What are the applications of Young's inequality?
+Young's inequality has numerous applications in mathematics, physics, and engineering, including calculus, linear algebra, optimization techniques, data analysis, and signal processing.
What are the generalizations of Young's inequality?
+Young's inequality has been generalized in various ways, including weighted Young's inequality, multivariate Young's inequality, and vector-valued Young's inequality, which have significant applications in data analysis, signal processing, optimization, and control theory.
How is Young's inequality used in optimization problems?
+Young's inequality is used to establish bounds and limits in optimization problems, particularly in the context of convex optimization, where one needs to maximize or minimize a function subject to certain constraints.
What are the future directions for research on Young's inequality?
+Future research directions include exploring new applications of Young's inequality, developing new generalizations and extensions, and investigating the relationships between Young's inequality and other mathematical concepts.
We hope this article has provided a comprehensive overview of Young's inequality and its significance in mathematics. If you have any questions or would like to learn more about this topic, please don't hesitate to comment or share this article with others.
